El rectángulo es una figura geométrica de gran importancia, presente en diversas disciplinas como la arquitectura, la ingeniería y las matemáticas. Calcular las dimensiones de un rectángulo es una tarea fundamental en muchos proyectos, ya sean de construcción, diseño o cálculos científicos.
Para llevar a cabo este cálculo, es necesario conocer las propiedades clave del rectángulo, así como las fórmulas y métodos para determinar su área, perímetro y longitud de los lados. Además, es crucial utilizar herramientas adecuadas y tener en cuenta consideraciones especiales en rectángulos no convencionales.
En este artículo, exploraremos a fondo la fórmula para calcular las dimensiones de un rectángulo, desde los conceptos básicos hasta ejemplos prácticos y consideraciones especiales. Aprenderemos cómo realizar cálculos precisos y comprenderemos la importancia de la exactitud en la medición y el cálculo de dimensiones en proyectos relacionados con los rectángulos.
Propiedades del rectángulo y conceptos básicos
Antes de adentrarnos en las fórmulas y los cálculos, es importante comprender algunas propiedades básicas del rectángulo. Un rectángulo es un polígono de cuatro lados, en el cual los ángulos interiores son todos de 90 grados. Esto significa que los cuatro ángulos del rectángulo son ángulos rectos.
Además, un rectángulo tiene dos pares de lados paralelos y congruentes entre sí. Esto significa que los lados opuestos del rectángulo tienen la misma longitud y son paralelos entre sí. Estas propiedades son fundamentales para realizar los cálculos precisos de las dimensiones del rectángulo.
Es importante mencionar también que el rectángulo tiene dos diagonales. La diagonal mayor es la línea recta que une los vértices opuestos del rectángulo, mientras que la diagonal menor es la línea recta que une los otros dos vértices opuestos. Estas diagonales también juegan un papel importante en el cálculo de las dimensiones del rectángulo.
Fórmulas para calcular el área y perímetro
Una de las dimensiones más importantes de un rectángulo es su área, que representa la cantidad de espacio que ocupa la figura en un plano bidimensional. El área se calcula multiplicando la longitud de la base por la altura.
La fórmula para calcular el área de un rectángulo es:
Área = Base x Altura
Donde la base es la longitud de uno de los lados paralelos y la altura es la distancia entre los dos lados paralelos restantes.
Por otro lado, el perímetro de un rectángulo es la suma de todos los lados. En un rectángulo, los lados opuestos tienen la misma longitud, por lo que el perímetro se calcula multiplicando la longitud de uno de los lados por cuatro.
La fórmula para calcular el perímetro de un rectángulo es:
Perímetro = 2 x (Base + Altura)
Es importante destacar que estas fórmulas son válidas únicamente para rectángulos convencionales, es decir, aquellos cuyos ángulos son rectos y que tienen lados paralelos y congruentes. En caso de tener un rectángulo no convencional, se deben considerar otros métodos de cálculo.
Métodos para determinar la longitud de los lados
En ocasiones, es posible que se conozca el área o el perímetro de un rectángulo y se desee determinar la longitud de los lados. En estos casos, se pueden utilizar fórmulas y métodos específicos para obtener los resultados deseados.
Si se conoce el área de un rectángulo y se desea determinar la longitud de los lados, se puede utilizar la fórmula del área para despejar la altura o la base, dependiendo de qué valor se conozca y qué lado se desee calcular. Por ejemplo, si se conoce el área y la base, se puede despejar la altura dividiendo el área entre la base.
Por otro lado, si se conoce el perímetro de un rectángulo y se desea determinar la longitud de los lados, se pueden utilizar fórmulas y métodos algébricos para encontrar los valores desconocidos. Por ejemplo, si se conoce el perímetro y la altura, se puede despejar la base utilizando la fórmula del perímetro y luego calcular los otros lados.
Ejemplos prácticos de cálculo de dimensiones
Para comprender mejor cómo se calculan las dimensiones de un rectángulo, veamos algunos ejemplos prácticos.
Ejemplo 1: Calcular el área y el perímetro de un rectángulo con una base de 8 cm y una altura de 5 cm.
En este caso, la fórmula para calcular el área es:
Área = Base x Altura
Área = 8 cm x 5 cm = 40 cm²
Para calcular el perímetro, utilizamos la fórmula:
Perímetro = 2 x (Base + Altura)
Perímetro = 2 x (8 cm + 5 cm) = 2 x 13 cm = 26 cm
Por lo tanto, el área del rectángulo es de 40 cm² y el perímetro es de 26 cm.
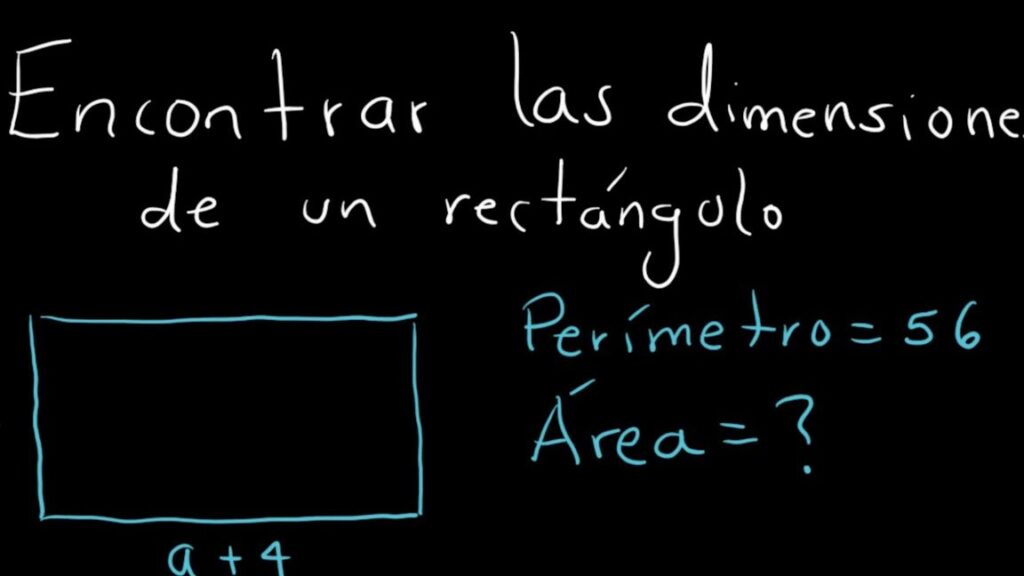
Ejemplo 2: Calcular la altura de un rectángulo con un área de 56 m² y una base de 8 m.
En este caso, utilizaremos la fórmula del área para despejar la altura:
Área = Base x Altura
56 m² = 8 m x Altura
Dividimos ambos lados de la ecuación por 8 m:
7 m = Altura
Por lo tanto, la altura del rectángulo es de 7 m.
Estos ejemplos nos muestran cómo aplicar las fórmulas y métodos para calcular las dimensiones de un rectángulo. Es importante recordar la importancia de utilizar las unidades correctas y de medir con precisión para obtener resultados exactos.
Consideraciones especiales en rectángulos no convencionales
En la mayoría de los casos, los rectángulos son figuras simples y convencionales, con ángulos rectos y lados paralelos y congruentes. Sin embargo, en algunas ocasiones, pueden surgir rectángulos no convencionales con diferentes propiedades.
Un ejemplo común de un rectángulo no convencional es un rectángulo con lados inclinados en lugar de ser paralelos y perpendiculares. En estos casos, las fórmulas y métodos tradicionales de cálculo de las dimensiones de un rectángulo no son aplicables.
En rectángulos no convencionales, es necesario utilizar métodos más avanzados como la trigonometría para determinar las dimensiones y ángulos. Esto implica medir ángulos y lados inclinados, utilizar funciones trigonométricas como el seno y el coseno, y resolver ecuaciones trigonométricas para obtener los resultados deseados.
Es importante contar con los conocimientos y las herramientas adecuadas para trabajar con rectángulos no convencionales y realizar los cálculos de forma precisa. En caso de duda, es recomendable buscar la asesoría de un experto en geometría o matemáticas.
Importancia de la precisión en la medición y cálculo
Para obtener resultados exactos y profesionales en el cálculo de las dimensiones de un rectángulo, es fundamental contar con medidas precisas y realizar los cálculos de manera precisa.
La precisión en la medición se logra utilizando herramientas adecuadas como reglas, cintas métricas y escalas especializadas. Es importante realizar las mediciones con cuidado, evitando errores como el desplazamiento de la regla o la cinta métrica, y asegurándose de que la medida esté alineada correctamente.
Además, es importante utilizar sistemas de unidades adecuados y convertir las medidas si es necesario. Por ejemplo, si una medida se encuentra en pulgadas y se necesita en centímetros, se debe realizar la conversión correspondiente utilizando un factor de conversión preciso.
En cuanto al cálculo de las dimensiones, es importante utilizar las fórmulas y los métodos correctos, así como realizar las operaciones matemáticas de manera precisa. Un error en los cálculos puede conducir a resultados incorrectos y afectar la precisión del proyecto en el que se trabaje.
Calcular las dimensiones de un rectángulo es una tarea esencial en diversos campos técnicos. Para llevar a cabo este cálculo de manera precisa, es necesario comprender las propiedades del rectángulo, las fórmulas y los métodos para calcular el área y el perímetro, y utilizar herramientas adecuadas como reglas y calculadoras. Además, en caso de rectángulos no convencionales, se deben considerar métodos más avanzados como la trigonometría. La precisión en la medición y el cálculo es fundamental para obtener resultados exactos y profesionales en proyectos relacionados con los rectángulos.